
Das Bin-Packing-Problem („Behälterproblem“) gehört zu den schwersten Problemen für Digitalrechner, die der Informatik bekannt sind. Es geht um die Fragestellung:
Gegeben sei eine Menge von Objekten bestimmter Größe und eine Menge von Containern mit einem bestimmten Fassungsvermögen. Gibt es eine Möglichkeit alle Objekte in den gegebenen Containern zu verstauen?
Auch wenn der Name und das hier verwendete Beispiel vor allem Anwendungen in der Logistik nahelegen, lassen sich durch Bin-Packing unter anderem auch Probleme der Routenplanung oder Ablaufsteuerung/Koordinierung ausdrücken. In diesem Beitrag betrachten wir zwei naive Lösungsstrategien für ein konkretes Beispiel des Bin-Packing und vergleichen, unter welchen Optimalitätskriterien die eine Lösung der anderen vorzuziehen ist.
Bin-Packing
Bin-Packing ist ein kombinatorisches Optimierungsproblem. Ganz allgemein zeichnet diese Probleme aus, dass sie nach einer ganz bestimmten Kombination problemspezifischer Entitäten suchen, sodass diese eine Wunscheigenschaft erfüllen: Beim Bin-Packing ist dies die Anordnung verschiedener Objekte mit bekannten Eigenschaften, sodass diese in die gegebene Menge an Containern passen.
In der Praxis ist man hierbei nicht nur an einer Ja-Nein-Antwort, also ob alle Objekte in die gegebenen Container passen, interessiert. Vielmehr ist von Interesse wie, das heißt in welcher konkreten Konfiguration, die Gegenstände in den Behältern anzuordnen sind. Aus ökonomischer Sicht ist es nachvollziehbar dabei nicht nur nach einer Lösung zu suchen, die die Objekte auf beliebige Art und Weise verstaut, sondern am besten auch so, dass so wenige Behälter wie möglich verbraucht werden. Genauso gut könnte aber auch die zur Verfügung stehende Zeit zum Verpacken begrenzt sein, sodass man einen Kompromiss zwischen Packdichte und Rechenzeit in Kauf nimmt.
Die große Schwierigkeit bei kombinatorischen Optimierungsproblemen besteht darin, dass im Vorhinein unbekannt ist, ob eine Konfiguration mit der gewünschten Eigenschaft überhaupt existiert. Genau so wenig weiß man, was die nächstbeste erreichbare Lösung ist. Um wirklich die optimale erreichbare Konfiguration zu finden, müssen daher alle möglichen Konfigurationen berechnet und verglichen werden. Die Menge der zu vergleichenden Kombinationen wächst dabei mit der Menge der zu kombinierenden Objekte exponentiell (oder stärker) an, sodass es unmöglich ist die nötigen Berechnungen für eine garantiert optimale Lösung auf Digitalrechnern durchzuführen. Daher nutzt man in der Praxis sogenannte Heuristiken. Diese versuchen durch geschickte Annahmen den Suchraum, also die Menge aller in Betracht zu ziehenden Konfigurationen, so einzugrenzen, dass sich möglichst viele gute und möglichst wenig schlechte Konfigurationen darin befinden.
Bin-Packing in 2D
Wir schauen uns in diesem Beitrag eine zweidimensionale Variante des Bin-Packing-Problems an, in der wir rechteckige Objekte in einen quadratischen 10×10 Container packen möchten. Es gelten dabei folgende Regeln: Die Objekte dürfen um 90 Grad gedreht werden. Ist ein Objekt einmal platziert, können wir seine Position nicht mehr ändern. Eine Konfiguration ist gültig, wenn sich die Objekte nicht überdecken oder über den Containerrand hinausragen.
Abbildung 1 zeigt den in diesem Beitrag behandelten Anwendungsfall:

Gepackte Container: Optimale Konfigurationen ermöglichen hier eine dichte Platzierung aller Objekte.
Die Abbildung zeigt zwei Container, die mit farbigen Objekten lückenlos (dicht) gepackt sind. Diese Konfiguration stellt eine optimale Lösung dar. Es lässt sich leicht erkennen, dass es mehrere dichte Konfigurationen, also mehrere optimale Lösungen gibt. Als Referenz: Das kleinste Objekt ist 1×1 Einheiten groß und das größte 6×5 Einheiten breit und hoch:

Objekte, die in zufälliger Reihenfolge aus den Containern geholt wurden.
Eine Entnahme der Objekte in zufälliger Reihenfolge und Rotation aus dem Container bildet nun den Ausgangspunkt für unser Anwendungsbeispiel.
Max-Rest und First-Fit Algorithmen
Anhand welcher Heuristiken können nun Konfigurationen erzeugt werden, die sich einer optimalen Konfiguration annähern? Wie bereits dargelegt, wollen wir versuchen die Container möglichst dicht zu bepacken. Zum anderen wollen wir auch den Zeitfaktor berücksichtigen.
Max-Rest-Algorithmus. Fangen wir mit der Überlegung zu einer zeitkritischen Anwendung an: Wenn in einem Container noch viel Platz ist, ist die Wahrscheinlichkeit hoch, dort ein Objekt platzieren zu können. Wir legen damit den Fokus darauf, möglichst selten ein Objekt in einem Container platzieren zu wollen, in dem eigentlich kein Platz mehr ist. So sparen wir Zeit. Über diese Motivation gelangen wir zum Max-Rest-Algorithmus. Dieser geht beim platzieren eines Objekts wie folgt vor:
Wähle den Container aus, der noch am meisten freien Platz zur Verfügung hat. Versuche das Objekt darin zu platzieren. Ist dies nicht möglich, nimm einen neuen Container und platziere das Objekt darin.
First-Fit Algorithmus. Wenn es nun wichtiger ist, einen Container möglichst dicht zu packen und dafür eine größere Anzahl von Rechenschritten zu investieren, könnten wir folgende Überlegung anstellen: Je öfter wir versuchen Platz für ein weiteres Objekt in einem bestimmten Container zu finden, desto höher ist die Wahrscheinlichkeit diesen dicht zu bepacken. Dieser Gedanke führt zum First-Fit Algorithmus. Bei diesem ist nun wichtig, dass die Container eine feste Reihenfolge haben. Der Algorithmus platziert die Objekte nach folgender Logik:
Gehe die Liste von Containern von vorne nach hinten durch. Platziere das Objekt in den ersten Container, in den es passt. Passt es in keinen Container der Liste, nimm einen neuen Container, platziere das Objekt darin und füge den Container hinten an die Liste der Container an.
Platzieren eines Objekts. Um die Ausgaben der Algorithmen nachvollziehen zu können, müssen wir noch festlegen wie genau ein Objekt in einen gegebenen Container platziert wird. Wir suchen in dem Container dabei wie folgt nach einem freien Platz:
Berechne alle freien Positionen in der Box. Ist die Fläche des zu platzierenden Objektes größer als die im Container insgesamt noch verfügbare Fläche, melde einen Fehler und brich ab. Gibt es noch genug freie Positionen, so gehe diese alle so durch, dass du die Position wählst, die am weitesten links und so weit wie möglich unten ist. Platziere die linke untere Ecke des Objekts auf dieser Position, wenn es sich dort nicht mit anderen Objekten überdeckt; falls es zu einer Überdeckung kommt, drehe das Objekt um 90 Grad im Uhrzeigersinn und überprüfe noch einmal auf Überdeckung. Kann das Objekt so auch nicht platziert werden, gehe zum nächsten freien Punkt. Hast du bereits jeden freien Punkt in dem Container probiert, melde einen Fehler.
Online Szenario
Wir präsentieren den verwendeten Algorithmen die Objekte zunächst in genau der Reihenfolge, in der wir sie oben zufällig aus den Containern geholt haben. Damit simulieren wir ein online Szenario, in welchem wir kein Vorwissen darüber haben, wie viele Objekte zu verstauen sind oder welche Eigenschaften (Größe) diese haben. Schauen wir nun, welche Konfigurationen wir mit Max-Rest und First-Fit finden. Das Ergebnis des Max-Rest Algorithmus sehen wir in folgender Abbildung:

Max-Rest-Algorithmus
Max-Rest schafft es, alle Objekte in 3 Containern unterzubringen. Es fällt auf, dass es in jedem Container noch große, zusammenhängende freie Flächen gibt (schwarze Punkte). In den Containern sind je [27, 25, 48] Einheiten frei. Der Algorithmus hat nur 2-mal versucht ein Objekt in einem Container zu platzieren, in den es nicht mehr hineinpasste (Fehlversuch).
Die Ausgabe des First-Fit Algorithmus sieht deutlich anders aus:

First-Fit Algorithmus
In jedem Container gibt es noch freie Punkte, aber die ersten beiden Container sind zu über 90% gefüllt. Dafür ist im Letzten nur ein einziges Objekt verstaut. Unter diesem Gesichtspunkt sind die Ergebnisse von First-Fit besser zu bewerten als die von Max-Rest. First-Fit passierten jedoch deutlich mehr, nämlich 11, Fehlversuche beim Platzieren der Objekte. Beide Beobachtungen sind zu erwarten. First-Fit schaut immer zuerst in den vorderen Containern nach, ob ein Objekt hineinpasst. Diese füllen sich über die Zeit. In der Folge können größere Objekte nicht mehr erfolgreich platziert werden, für die kleinsten Objekte hingegen wird der letzte freie Platz genutzt.
Offline Szenario
Wir haben eben unter der Annahme gearbeitet, nicht zu wissen, welche oder wie viele Objekte zu verstauen sind. Schauen wir uns zum Abschluss nun noch den offline Fall an. In diesem gehen wir davon aus, dass wir die Menge der Objekte im Vorhinein kennen und diese vorverarbeiten dürfen. Eine sehr einfache Vorverarbeitung wäre eine Sortierung der Objekte, zum Beispiel absteigend nach Größe. Sortieren wir die Objekte nach Flächeninhalt und Breite, erhalten wir folgende Reihenfolge:

Die zu verpackenden Objekte sortiert nach Fläche und Breite
Wenden wir nun wieder die beiden Heuristiken an. Abbildungen 6 und 7 zeigen jeweils das Ergebnis des Max-Rest und des First-Fit Algorithmus auf der sortierten Liste. Letzterer wird bei Anwendung auf eine sortierte Liste auch als First-Fit-Decreasing Algorithmus bezeichnet.
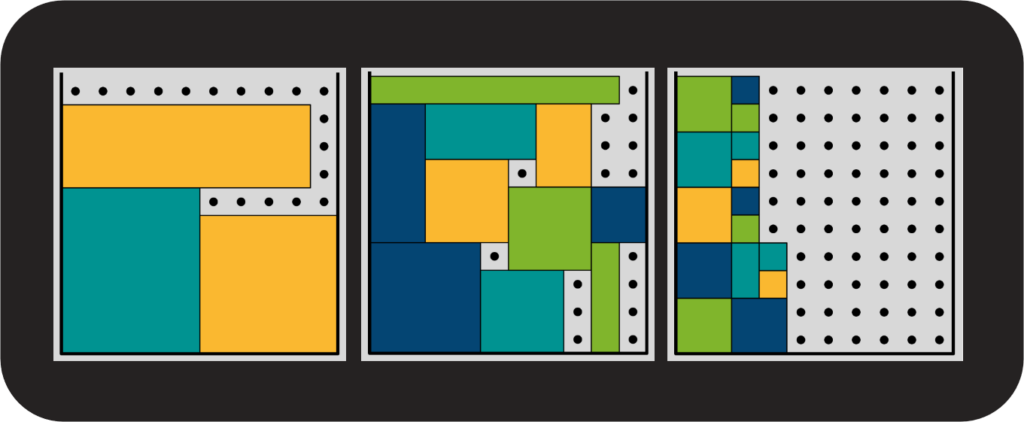
Ergebnis von Max-Rest auf sortierter Liste

Ergebnis von First-Fit auf sortierter Liste (First-Fit-Decreasing)
Beide Algorithmen liefern erneut je drei Container zurück. Bei Max-Rest sind in den Containern noch je [18, 16, 66] Positionen frei. Die Auslastung der ersten beiden hat sich also erhöht und im Letzten ist mehr Platz frei geworden. Dabei hat der Algorithmus erneut nur 2 Fehlversuche bei der Platzierung durchlaufen.
Der erste Container von First-Fit-Decreasing sieht dem von Max-Rest sehr ähnlich. First-Fit-Decreasing hat es allerdings geschafft, die länglichen Lücken restlos aufzufüllen und den Container dicht zu packen. Die verbleibende Kapazität der Container beträgt je [0, 12, 88]. Die Auslastung des zweiten Containers hat sich folglich leicht erhöht, die des letzten leicht verringert. Die Anzahl der Fehlversuche der Platzierung beträgt 22, das entspricht einer Verdoppelung. Auch das ist mit einem Blick auf den ersten Container erklärbar. Dieser war mit den größten drei Objekten bereits so sehr befüllt, dass nur die kleinsten Objekte noch Platz darin fanden. Diese wurden aber erst ganz zum Schluss einsortiert, der Algorithmus hat also für alle Objekte mittlerer Größe erfolglos versucht diese in den ersten Container zu packen.
In der Tabelle fassen wir noch einmal die gesammelten Statistiken zusammen:
| Algorithmus | Freie Kapazität pro Container | Anzahl Fehlversuche bei Platzierung |
| Max-Rest | [27, 25, 48] | 2 |
| First-Fit | [3, 6, 91] | 11 |
| Max-Rest sortiert | [18, 16, 66] | 2 |
| First-Fit sortiert | [0, 12, 88] | 22 |
Die Objekte vorzuverarbeiten hat bei beiden Algorithmen geholfen die Container dichter zu packen. Dabei hat es First-Fit geschafft einen Container lückenlos zu füllen. Ist Zeit ein begrenzender Faktor, empfiehlt sich gemäß dieser Analyse eher der Max-Rest Algorithmus, weil es bei diesem zu deutlich weniger Fehlversuchen gekommen ist.
Durch geschicktes Raten gut kombinieren
In diesem Beitrag haben wir gelernt, dass kombinatorische Optimierungsprobleme auch in Zukunft unüberwindare Hürden für unsere Digitalrechner darstellen werden. Die beste Handlungsempfehlung ist in diesem Fall geschickt zu raten. Dabei erhalten wir zwar nicht unbedingt die optimale Lösung, aber solche Ansätze können durchaus akzeptable Ergebnisse liefern. Konkret haben wir das Bin-Packing genauer betrachtet und die zwei naiven Lösungsstrategien Max-Rest und First-Fit in einem online und einem offline Szenario verglichen. Weitere naive Strategien wären der Next-Fit und der Best-Fit Algorithmus. Auch evolutionäre Algorithmen liefern gute Heuristiken und finden praktische Anwendung. Eine solche Anwendung findet sich in dem Blogbeitrag „Evolutionäre Optimierung von Quantenschaltkreisen„, der sich mit jener Hardware beschäftigt, die kombinatorische Optimierung potenziell traktabler machen könnte.
ML2R Autumn School 2021
Kombinatorische Optimierung ist kein übliches Anwendungsgebiet für Verfahren des Maschinellen Lernens. Auf der diesjährigen ML2R Autumn School bieten wir vom 04.-08. Oktober einen Rahmen für motivierte Masterandinnen und Doktorandinnen, um kreativ über Möglichkeiten nachzudenken, Verfahren des Maschinellen Lernens auf kombinatorische Strukturen anzuwenden. Der Fokus wird auf einer wohldefinierten Version des Bin-Packing-Problems liegen, an dem in Kleingruppen praktisch gearbeitet wird. Die Teilnahme an der Autumn School ist kostenlos, die Anzahl der Plätze jedoch begrenzt. Bewerbungsschluss ist der 29. August.
